Counting to 481,008,528
Joseph L. — May 07, 2019
Introduction
481,008,528. That’s the number of unique team compositions that exist in League of Legends as of Patch 9.9. At 20 minutes per game, it would take over 18,000 years to play all of them. Thankfully, we don’t need to play that many games to count them: with a bit of math, we can determine this number with a simple calculation. In fact, using just a few ideas required to count the number of team compositions, we can solve all kinds of different counting problems. In this article, we’ll show how to compute solutions to a variety of League-based counting problems, from pick order to team composition. To get there, we begin by exploring the key ingredient to solving these counting problems: the factorial.
Factorials: Ordering Things
Let’s say we’re loading into the game. Our champion has three core items that are must-buys, but the build order is flexible, so we wonder: how many orders are there? To figure this out, we could write a list of every possible sequence of the three core items and count them, but there’s a much less time-consuming way to determine that number: a factorial. Factorials are denoted by , read as
“ factorial,”
where is
a nonnegative integer, like 0, 1, or 144.
Using to represent a nonnegative integer, factorials are defined as follows:
In other words, means that we take , multiply it by , then multiple that by , all the way down until we get to 1. For example, .
As it turns out, is also the number of different ways we can order items. So let’s say our team knows what 5 champions they want to play. Then the factorial tells us how many possible orders we could pick those 5 champions in. In this case, , so we have
Now we know how to use the formula—but why does formula tell us the number of ways to order things? To understand this, let’s return to the example of ordering three items.
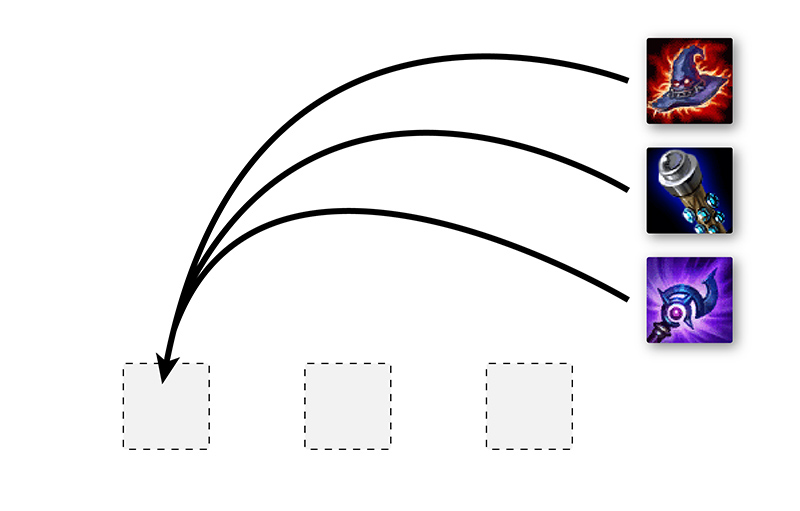
There are three ways to choose the first item.
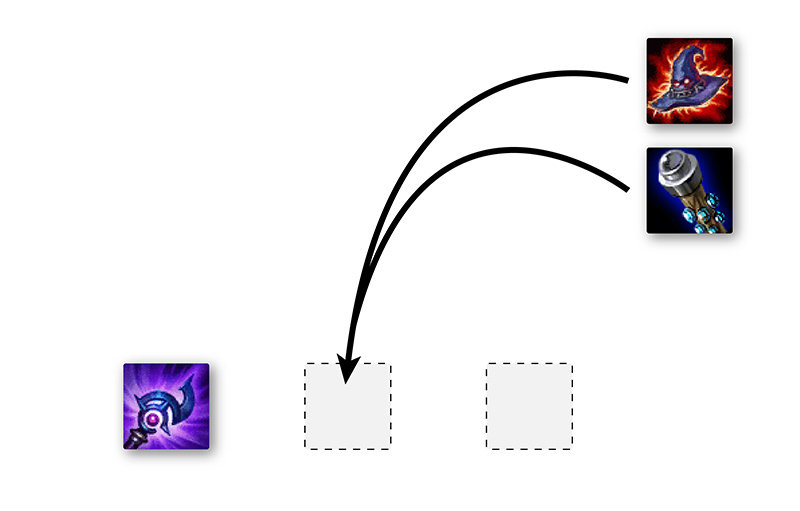
Once the first item is chosen, there are two ways to choose the second item.
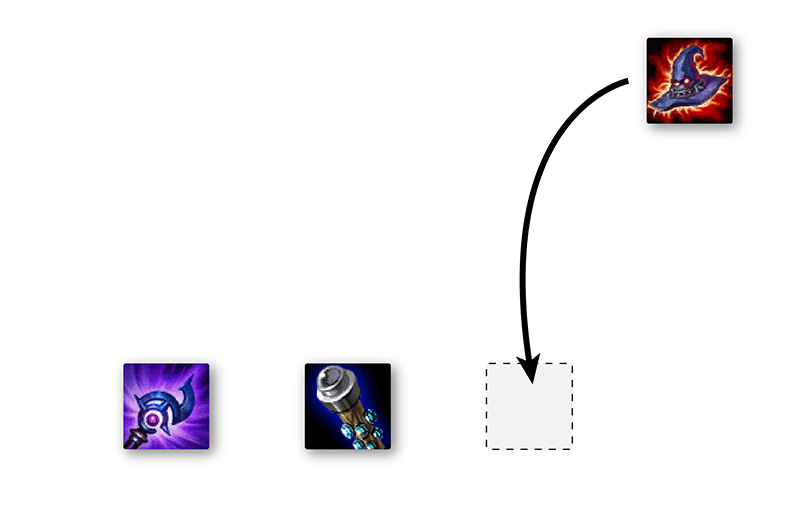
Once the first two items are chosen, there's only one option for the last item.
When choosing the first item in our build order, we have three items to choose from. Once we select an item, we now have two choices for the second item in our build. After this choice, we place the last item in the final slot our build order. Over the course of finalizing our build, we had 3 options, then 2 options, and then 1 final option.
We need to multiply these numbers so that we count each possible sequence of items that we could have chosen: for each of the three possible first item choices, there are two more options after that, then each of those options is followed by one option (the last item). So each of the initial three options leads to two more, down the road. Adding them up, we get . Then we count the final item selection in each of these choices: there is 1 option, so we multiply to get the final answer. In total: .
Looks familiar right? It’s the factorial we just learned!
Check-Your-Knowledge Question
- It’s the end of the game and the top laner is full build. How many ways could they order the items in their inventory?
Show answer - Since we already know what
is, notice that we can write
as a quicker way to calculate .
(Try expanding both sides if you don’t believe it.) Can
you turn this into a general statement about the value of
, if
is an
integer greater than 1?
Show answer
Combinations: Choosing Things From
With the power of the factorial, we’re one step away from answering how many possible team compositions exist in League. To do this, we will use a combination, which says “how many ways can things be chosen from things.” In the language of the team composition question, this becomes “how many ways can we choose 5 champions for a team out of 144 total champions in the game.” This may seem daunting at first, but the formula turns outs to be a simple and beautiful extension of our knowledge of factorials.
Before getting to that, let’s define the combination:
The notation , read as “ choose ”, gives us a short way of referring to the expression on the right, which involves several factorials. The cool thing is, this expression happens to be exactly the number of ways to pick things from .
For example, there are currently 14 champions in the free rotation roster. How many unique team compositions can we make from this group? In other words, how many ways can we pick 5 champions out of 14? Our new formula tells us that
Notice that combinations are not concerned with the order in which champions are picked, just the possible teams we can end up with.
Now that we’ve seen an example, let’s break the combination formula down. Suppose we have champions and are going to choose of them. We want to show that the number of possible ways to do this is given by the formula for .
To figure this out, it helps to think about what each factorial in the formula is counting. Imagine we picked champions by lining up all of our champions in a row and placing a wall to separate the champions we want in the group from the remaining champions, as shown in the picture below.
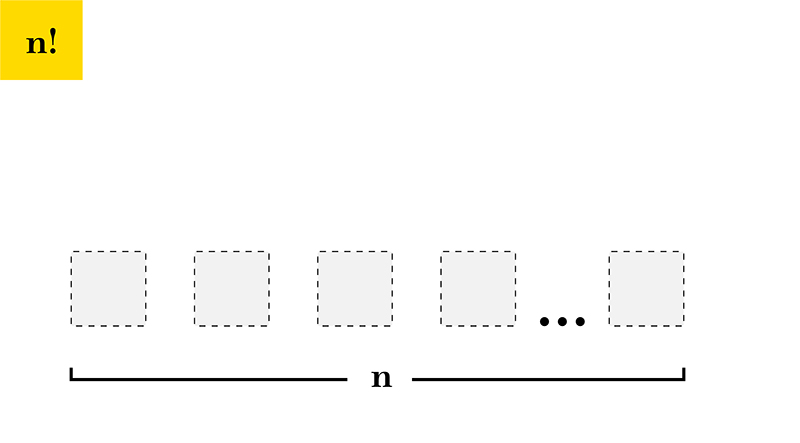
There are n! ways to order all n champions.
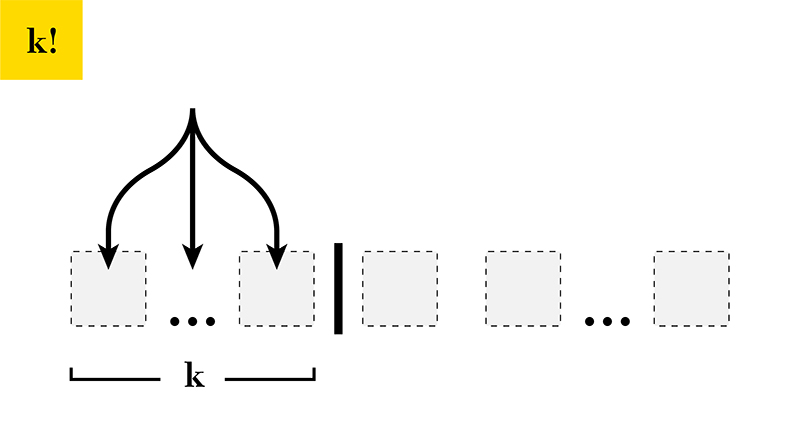
Once k champions are on the left of the wall, they can be reordered in k! different ways.
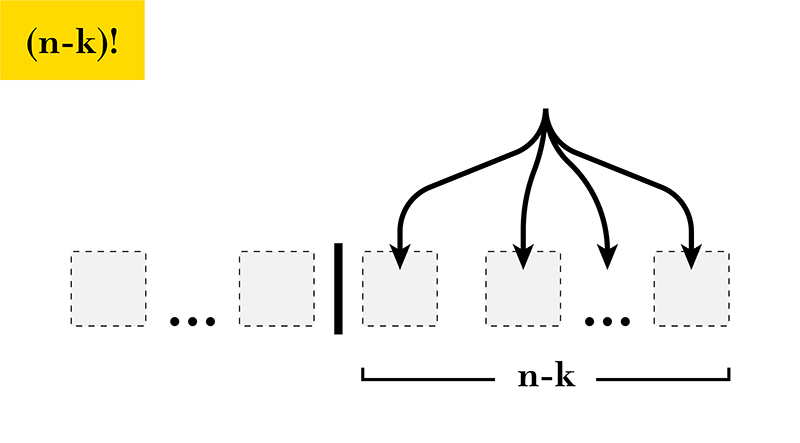
Once k champions are on the left of the wall, the remaining n-k can be reordered in (n-k)! ways.
From earlier, we know there are possible ways to line up all champions. Now suppose we kept the wall in the same place and reordered all champions. This reordering can give us a new group by placing a different set of champions on the left of the wall. In fact, any possible group of champions can be formed this way. (Can you see why?)
So, to count the ways to choose champions from , we simply need to count the number of unique ways to put champions on the left of the wall. However, we need to make sure we don’t double-count any groups, since there are many possible re-orderings of the champions that leave the same on the left. We need to take the total ways of ordering the entire line, and divide it by the number of ways we can get the same group of champions on the left.
For a single group of champions, there are ways they could be ordered on the left of the wall, and there are ways the remaining champions could be ordered on the right of the wall. To account for this, we have to divide the total number of orderings by so that each group of is only counted once, instead of being counted times each. This operation creates the same formula we saw above:
This is why the formula for counts the number of ways to pick things from .
Check-Your-Knowledge Question
- C9 Sneaky starts the game with two Doran’s Blades and nothing else in his inventory. How many ways could he place those in his inventory?
Show answer - Verify that .
Can you generalize this statement to be about
?
What is an intuitive explanation of this fact?
Show answer
Closing Questions: Put It All Together
- As of January 25, 2019, there are 144 champions in LoL. How many unique team compositions can be made?
Show answer - How many possible team composition matchups are there (assuming that no champion can appear on both teams)?
Show answer
Going Further
Now that we understand the basics of combinations and how they function, we can begin to solve complex problems with a little help from other mathematical concepts.
Permutations: Counting Ways to Pick Things in Order
A combination counts the number of ways to choose a subgroup of a certain size from a larger group, when we don’t care the order in which elements are selected. By modifying the formula for the combination, we get a formula that counts the number of ways to pick and ordered list of elements from .
If this sounds familiar, it’s because we just defined the permutation! Can you prove that this counts what we said it does? (Hint: you can use a similar argument to the one used for the combination.)
Vandermonde’s Identity
Vandermonde’s Identity is a nice example of two different ways to count the same thing. Suppose we have two groups, of size and , and we’d like to pick people total from between the two groups. How many ways can we do this? Of course we know will give us the answer, based on our earlier result about combinations. Vandermonde’s Identity gives an equivalent expression for this that may not be obvious at first:
where and are the sizes of the initial groups while is the size of the group you want to create.
To better understand Vandermonde’s Identity, let’s look at an example. The current number of Ionian and Noxian champs in league as of Patch 9.9 are 18 and 11 respectively. How many unique team compositions (groups of 5 champions) could we come up with using only Ionian and Noxian champions?
Plugging into the left side of the formula, we get . Using what we know about factorials, we could get the answer this way. However, using Vandermonde’s Identity, we can translate the binomial into the summation . Let’s break this down into pieces.
The summation separates the original binomial into sums of products of smaller binomials. In each expression, the first binomial is the number of ways to pick Ionian champions. The second binomial is number of ways to pick Noxian champions. The summation lets us add up each of these for every possible number of Ionians are chosen. In total, there are 462 ways to create a group with 5 Ionians, 5940 ways to create a group with 4 Ionians and a Noxian, 25,245 ways to create a group with 3 Ionians and 2 Noxians, 44,880 ways to create a group with 2 Ionians and 3 Noxians, 33,660 ways to create a group with an Ionian and 4 Noxians, and 8,568 ways to create a group with 5 Noxians, for a total of 118,755 unique combinations of Ionian and Noxian champions.
Multinomials
How many ways can we choose a group of size and a group of size from objects? By applying similar reasoning used in the section on combinations, we obtain the multinomial coefficient:
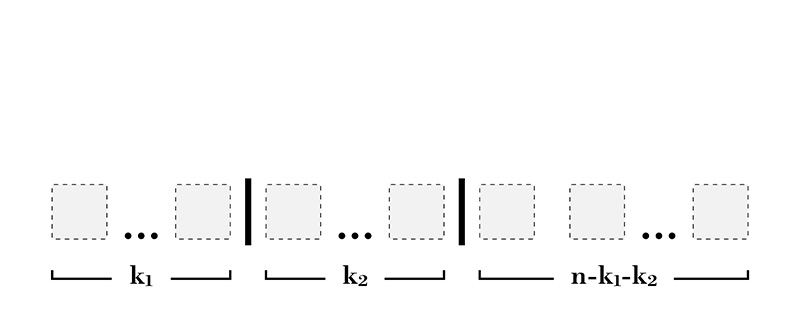
Placing 2 walls to create a group of size and a group of size , there are orderings that leave the same champions in their group and the same champions in their group.
This can be applied for any number of groups, as long as the as long as the total size of the groups is less than or equal to .


